On the principle -that mistakes in reasoning are often more instructive than correct deductions are, some common and typical fallacies are examined. 'Fallacies' are errors in reasoning.
1) Irrelevant conclusions
When the conclusion bears no relation whatever, or only superficial
relation, to the premises it is obviously invalid, whether true or false.
This is sometimes termed 'non sequitur' ('does not follow').
Eg. If the Minister of Transport declared that fares would be doubled
and the doubling of fares was against the wish of the Unions and the
public then the Prime Minister therefore removed the Minister of Transport
from his job. If this seems reasonable, consider that the Prime Minister
could have acted as stated for many other reasons.
2) Undistributed Middle Term
This error in reasoning occurs both where invalid and valid logical
syllogisms are involved.
With invalid logical syllogisms undistribution occurs when the middle
term is not entailed by both the logical subject and the logical predicate.
Egs:-
If no S = M as
in 'If no U.S. presidents were females (TRUE)
and no P = M and no U.S. generals
were females (TRUE)
then no S = p then no
U.S. presidents were generals (false)
Correct representation of the above by Venn's diagrams would be:-
| either | 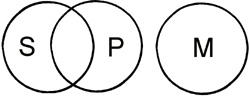 |
We see the middle term entails neither S nor P, while S can be partly included in P in the above concrete example. |
| or | 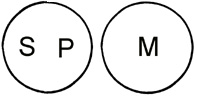 |
Going by the structure alone, S and P could just as well be exactly equivalent, without being included at all under M. |
Therefore we have a case of undistributed middle term through an invalid
syllogism. This shows that no conclusion follows from two universally
negative premises.
With valid logical syllogisms the middle term can be undistributed
when it has two different interpretations, _the one of which applies
only to the subject and the other only to the predicate as follows:
(Note. Many books on logic regard the first case of undistributed middle term above as invalid due to two universal negative premises and thus do not include this type of fallacy as undistribution).
| If all S
are M and no M are P then no S are P |
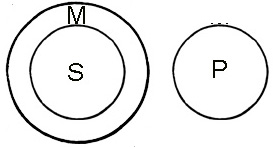 |
An invalid conclusion occurs
due to the middle term's two different interpretations in:
If all humans are equals
and no equals are different from one another
then no humans are different from one another
The middle term 'equals'
can be interpreted as 'being due the same rights and duties' in relation
to the logical subject 'All humans', and as 'being of the same nature'
in relation to the logical predicate 'not being different from one another'.
Therefore, if the above differences in interpretation apply, as is likely,
the conclusion does not follow; The term 'equals' is undistributed.
This can be represented by Venn's diagram as:
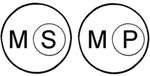 |
where two different middle terms are actually involved. |
This type of error is very common, like the cases of pseudo-agreement and pseudo-disagreement discussed earlier, the troublesome term is conflated, which is to say, combines two meanings into one with confusing results.
3) Inconsistent use of copulas
The copula (verb or verbal phrase which connects the subject
and predicate of a statement) must express the same concept in the
conclusion as it does in each of the premises. If not a combination
of irrelevant conclusion and undistributed middle term can arise, (in
modern logic the copula is regarded as part of the logical predicate
of a premise or conclusion, hence it is usually included under the middle
term). For example:-
(a) If all bishops have some responsibilities'
(b) and all responsibilities 'are sometimes a problem'
(c) then all bishops 'are sometimes a problem' The predicates are indicated
by single apostrophes above. The copula is underlined in each statement.
The logical structure of the syllogism is valid as in:
| (a) If all
S = M (b) and all M = P represented as:- (c) then all S = P |
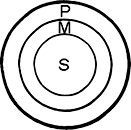 |
The copula 'have' in the major premise is changed to 'are' in the conclusion. This also makes an additional fallacy of undistributed middle term. 'have some responsibilities', being replaced by 'all responsibilities' in the minor premise and for an irrelevant conclusion,
4) Inconsistent use of descriptive and prescriptive statements
This is a special case of 3) above.
One cannot logically derive a prescriptive (or normative) conclusion
from two descriptive premises, or vice-versa.
For example:-
(a) If all societies are imperfect If
all S = M
(b) and what is imperfect is possible to improve and
all M = P
c) then all societies ought to be improved. then
all S ought to = P
This is an invalid conclusion. Though this seems reasonable enough,
the conclusion introduces a normative concept that is not explicit in
either of the premises. One cannot logically deduce any prescriptive
norms of action (i.e. what should, must or ought to be) from descriptions
of what is the case,
Eg: Someone says: "Good actions ought to be praised, but praise
occurs less commonly than it could, proving good action less common
than it could be." We have here a descriptive conclusion from two
prescriptive premises. To see the whole argument more clearly it can
be made more explicit in syllogistic form. The syllogism is the same
structure as above, though its grammar varies from the spoken words.
(a) If all good actions ought to be praised (Prescriptive major premise)
(b) and what "ought to be praised is a less common occurrence than
it could be (Prescriptive minor premise).
(c) then all good actions are less common than they could be. (Descriptive
conclusion)
From the above we see that one cannot discover what is the case from
norms that state what ought to be (prescriptive statements). "This
is a. special case of inconsistent use of copulas ('ought to be' being
illegitimately replaced by 'is' in the conclusion). From the viewpoint
of logical form, the syllogism would give a valid conclusion if the
copulas had been consistent.
Note that normative conclusions can be validly deduced, from one
descriptive and one normative premise, as in the valid, syllogism,
as follows:-
(a) If by accepting the Unitarian
ethic we ought to respect all fellow beings
(b) and respecting all fellow beings is also to recognise human rights
(c) then by accepting the Unitarian ethic we ought also to recognize
human rights.
5) Circular proof
This fallacy occurs when one or both of the premises are dependent for
their eventual truth on the truth of the conclusion itself. Though the
conclusion follows from the premises and thus amounts to logical proof,
it has already been assumed true at the start. This form of fallacy
is therefore frequently called pseudo-argument or pseudo-proof.
For example:- If all that has existence has measurable mass and vice-versa and only matter has measurable mass then only matter has existence.
This appears to fulfill all the conditions of logically valid deduction.
When we consider the term 'having measurable mass' we realise that the
conclusion 'matter' is simply another word for the same concept. Nothing
has been proven, only a new word substituted in the conclusion, so that
the assertion of the major premise and conclusion are equivalent in
meaning. This example is based on the assumption that 'having measurable
mass' and 'matter' are used in the normal way, where the one is a definition
of the other. If, however, 'matter' were being used in a different sense
(such as the 'matter' that comes out of an infected wound), the circularity
would disappear. But then the argument would be all the more unreasonable
from the common sense point of view.
A circular proof is biased in favour of the conclusion from the start
as can be seen in the following argument, particularly because the hypothetical
'if a then': Eg: 'The President's statements cannot be called into question,
and cannot be other than true because only what can be called into question
can be false'.
When the argument is ordered as a syllogism we get:
(a) (if), the President's statements cannot be called into question
(b) (and) what cannot be called into question cannot be other than true
(c) (then) the President's statements cannot be other than true.
The circularity of the argument hinges upon the term 'not be called into question'. This usually means 'beyond doubt' or 'reliably true'. Hence the conclusion tells us no more than the major premise. However, taken literally, it could possibly mean 'not right to doubt' or even 'futile to attempt to contend' which would then give the fallacy of undistributed middle term in addition to circularity. Circular proof is frequently compounded with other fallacies, chiefly with ambiguity of meaning due to insufficient precision, especially in the middle term.
6) Invalidity due to one implicit premise
In actual argument people frequently abbreviate the chain of reasoning
by leaving one of the premises unstated, assuming it to be understood
and unnecessary to state because of its apparent obviousness. When the
missing premise is subsequently supplied it may be found that the argument
is not a logical deduction. Either the structure may be seen to be invalid,
the middle term undistributed, the premise false or the argument circular.
Consider the argument that has been heard frequently during economic
recessions in the EU and the U.S.A.
Eg; 'The State will not create jobs for those who are without the initiative
to find employment themselves because they are unproductive for the
economy of the country.'
The stated argument contains a logical subject, predicate and one 'middle
term' .When it is explicated in full, supplying the implicit premise
we get:-
(a) (If) the State will not create jobs for those who are unproductive
for the economy of the country
(b) (and) those who are unproductive for the economy of the country
are those who are without the initiative to find employment themselves
(c) (then) the State will not create jobs for those who are without
initiative to find employment themselves.
The above argument's logical structure is valid:-
(a) If all S = M (Major premise)
(b) and all M = P (Minor premise)
(c) then all S = P (Conclusion)
The unreasonability of the
argument becomes more evident when the implicit minor premise is made
explicit. Not only is it likely that the minor premise is false, making
the conclusion necessarily false, but it also makes the assumption that
those who are unproductive, presumably because they cannot find jobs,
also cause the lack of jobs through lacking initiative on their own
part. This helps to demonstrate the inherent circularity of thought
in the argument: the State will not create jobs for those who are unproductive
because they are unproductive in having no jobs, the State being unwilling
to create any, apparently on the grounds that jobs only arise from the
individual initiative of job-seekers.
Eg. All adults are incapable of stable emotional relationships who have
been deprived of love in childhood because some of them cannot get adequate
satisfaction for their need of basic trust.
By making both premises explicit we get:-
(a) If some who have been deprived of love in childhood are adults who
cannot get adequate satisfaction of their need for basic trust
(b) and all adults who cannot get adequate satisfaction of their need
for basic trust are incapable of stable emotional relationships
(c) then all (adults) who have been deprived of love in childhood are
incapable of stable emotional relationships.
This is evidently an invalid syllogism because the major premise is
qualified by the limited 'some':-
| (a) If some
S = M (b) and all M = P (c) then all S = P |
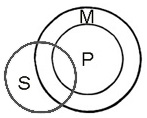 |
Note that the actual conclusion is not unproven by the premises, but remains unproven, and that it would be valid if restricted to 'then some S = P'. The conclusion 'all S = P' could also be true (though invalid) if other causes were found for those cases excluded by the premises (providing the premises were also true), or it could be false (provided that the premises are false and no other causes exist).
7) Tendentious arguments
Another sort of fallacy to be examined here are arguments tending
to persuade towards an invalid conclusion by irrational means. The
number of ways this can be attempted are too many to list and too diverse
to classify in detail satisfactorily. Examples of some of the more common
types are chosen.
Tendentiousness also occurs in evading an issue to conceal lack of
logical validity.
An example of evading an issue has already been given under 6) above.
When this occurs in" support of an invalid conclusion, this is
a tendentious argument. Other methods of doing this are by supplying
irrelevant and obscure reasons, making use of pseudo-agreement or pseudo-disagreement
to conceal the actual meaning intended by a premise, or doing so by
purposefully unclear and insufficiently precise terms. Evasion of issues
can also be achieved simply by refusing to provide the necessary premise
to show an argument's invalidity or by giving reasons why this is unnecessary
or pointless so as to cover up the shortcomings of a conclusion.
8) Character smudges
whereby one argues against a person rather than a standpoint, so diverting
attention to the character or characteristics of the one argued against
instead of to the actual argument. This is an important variation of
evasion of the issue. It is also a case of making irrelevant arguments
on an issue. (This is to be treated more thoroughly under the subject
of 'relevance to an issue'). A blatant example is sufficient at this
stage: Eg; "Mr. Black argues that big international monopolies
cause world shortages, but this is untrue, Mr. Black being well-known
for his 'off-white' anarchic views."
Additionally, the pun on the name 'Black' tends to divert attention
and make a joke of a serious view, so it is also emotionally tendentious.
The example seems to be an argument but in fact is no argument at all,
rather a case of sheer demagogy.
9) Purposeful use of untrue premises
The more false statements or lies that are compounded in an argument,
the more difficult the whole becomes to refute in clear, concise terms.
Criminal techniques of 'framing a case' employ such methods, as well
as political demagogues who make completely false statements seem more
feasible by presenting them within an otherwise valid logical framework.
10) 0pen and veiled threats
Threats are emotive in intent even if not expressed in emotive terms.
They constitute irrational purposes when used in the context of apparent
reasoning.
Eg: "Those who do not agree that human rights are fully observed
in this country are those who break the law of this country, and lawbreakers
oust be investigated and imprisoned.'
This might imply a veiled threat against arguing opponents. Consider
also the case of a schoolmaster who asserts:-
'The Bible says an eye for an eye and a tooth for a tooth, which means
that revenge is just and anyone who argues any more will get a punch
in the face.'
This type of fallacy was amusingly termed 'arguments with a stick' (argumentum
ad baculum) in traditional textbooks. Likewise what I would call
'arguments with a carrot' can also occur where the threat is the loss
of some reward or inducement used as part of an argument:-
Eg; If this country remains in the EU, it will lead to higher profit
for everyone here. As a large investor in this country I say it will
also lead to high profits for us financiers but if this country does
not remain in the EU, it will lead to our having to remove our investments
to the loss of higher profit for everyone here. Though the structure
of this argument is complex, its inducement and veiled threat are apparent.
This is sufficient to invalidate it as rational proof, even though it
may prove true in the course of events.
EXERCISES (LOGICAL FALLACIES)
In the following exercises
there may be a fallacy or there may not. These exercises therefore serve
to test one on the principle of valid inference. - If no fallacy is
found, give a brief account of why you consider the argument 'valid.
Rely if necessary upon the use of Venn's diagrams. If you discover fallacies,
state which ones you consider them to be giving reasons with reference
to the fallacies listed above:-
1) All dogs are canine-teethed animals
and all canine-teethed animals are mammals,
therefore all dogs are mammals.
2) All dogs are mammals
All mammals are warm-blooded
Therefore all dogs tend to bark.
3) Mrs. Jones is a snob
Most snobs are bores
Therefore Mrs. Jones is a bore.
4) If children ought to be
heard and seen
and those who ought to be heard and seen are adult's
therefore children ought to be adults.
5) Those who agree with the State policy of making financial profit in industry more important than the improvement of dangerously unhealthy working conditions are only being sensible. Any fool can see that industries will eventually fail if they do not make financial profit most important of all.
6) If no accomplished musicians
cannot improvise
and no accomplished actors cannot improvise
then no accomplished musicians cannot be accomplished actors.
7) What is good cannot also
be bad and what is bad cannot also be good
therefore what is good is good.
8) If those who suffer from
mental derangement ought to be given mental treatment
then those who prefer unemployment to work ought to be given mental
treatment.
9) If everyone is not the
same
and what is not the same is different
then everyone is different.
10) Some blondes prefer gentlemen
Some brunettes prefer gentlemen
and therefore some blondes prefer brunettes
11) All those who have $1
million are rich
and all the rich are people who have nothing but wisdom
then all those who have $1 million are people who have nothing but wisdom.
12) If R. Priddy is making
use of political examples in his textbook on semantics and logic
and R. Priddy is a person who has political views that are suspect and
doubtful
Therefore it is evident that his textbook does not present the logical
materials neutrally and is politically suspect and doubtful.
13) If all the class of p
is included in the class of q
and all the class of q is included in the class of r
and all the class of r is included in the class of s
and all the class of s is included in the class of t
and all the class of t is included in the class of u
then all the class of u is included in the class of p.
14) If all those who disagree
with established authorities are suffering from psychological complexes
and all those who disagree with established authorities are those who
themselves are capable of making up their own minds,
then all of those who think themselves capable of making up their own
minds are suffering from psychological complexes.
15) Consider the above argument
with the following altered conclusion:
then some of those who think themselves capable of making up their own
minds are suffering from psychological complexes.
SOLUTIONS TO EXERCISES IN LOGICAL FALLACIES
1) Let 'dogs' = 3, 'mammals'
= P and 'canine-teethed animals' = M:-
If All S are M & All E are P then All S are P Valid.
2) Irrelevant conclusion
(non sequitur)
3) If S is M where S = 'Mrs. Jones', M = 'snobs' and P = 'bores' &
some M are P then S is P (invalid/undistributed middle term)
4) Let 'children's S, 'those
who ought to be seen and heard' = M & 'adults' = P, then the logical
form is:- If all S are M & all M are P then all S are P. This is
a valid logical form. However the copula is altered in the conclusion)
from 'are' in the premises (as abstracted above) to 'ought to' in the
conclusion. This would constitute inconsistent use of copulas thus lead
to invalidity.
It could be argued, however, that the method of formalisation required
for syllogistic abstraction leads to alteration of the assertion in
the first premise 'If children ought to be seen and heard'. This bears
a different sense to 'If children are those who ought to be seen and
heard'. The first formulation has a prescriptive form, the second a
descriptive form. If the first premise is left in its original form
(i.e. 'If all S ought to be M') we then have two different middle terms:-
'heard and seen' and 'those who ought to be heard and seen'. This leads
to the fallacy of undistributed middle term. Whichever solution is chosen,
the argument remains invalid. (The conclusion cannot be derived logically
from the premises.)
5) The conclusion uses emotive
language, which is unclear and does not allow of secure translation
into logical language (i.e. logical form). However, if 'Any fool' were
interpreted as 'those who are only being sensible' (which is an interpretation
open to argument), we still would be unable to formalise the whole in
logical terms, for there are no clear premises leading to a clear conclusion.
There is no logical argument at all. What appears as an 'argument' is
merely the assertion of norms.
6) Let 'accomplished musicians' = S 'accomplished actors' = P and 'those
who cannot improvise' = M. Then the logical form is:- If no S are M
and no P are M then No S are P (invalid syllogism).
That both S and P are excluded from M does not prove them to be mutually
exclusive classes.
7) Circular reasoning. There is no middle term, there is no predicate in the 'conclusion'. The 'conclusion' simply affirms a valid analytic statement "What is good is good". This does not follow from the proceeding statements, but is an assumption inherent in both of them.
8) Let 'those who suffer
from mental derangement' = S
and 'those who prefer unemployment to work' = P
and 'those who ought to be given mental treatment' = M
then we have:-
If S are M, then P are M. This is an argument where the minor premise
is implicit (left unstated). What is implied here then is that:- If
S are M and P are S, then P are M.
Though the syllogism is valid, and the conclusion follows from the premises
in a formal sense, the 'missing premise' is most likely to be false:-
i.e. 'and P are S' means 'and those who prefer unemployment to work
are those who suffer from mental derangement'. This implicit premise
appears "to be less innocuous when not made explicit. Its falsity
being apparent, one can readily see that the conclusion does not therefore
have to be true also. A further complication in this type of pseudo-argument
is that the premise and conclusion forwarded were not descriptive statements.
Only by a doubtful traditional method of translation could they be made
descriptive in form. This tends to lend an air of logicality to such
normative statements which they otherwise would not possess.
9) The term 'the same' is most probably interpreted differently in each of the premises. Without a clearer determination of what 'the same' means in the first premise, its truth cannot be judged. Therefore the truth of the conclusion, though it follows logically from the truth of the premises, cannot be materially guaranteed. The form of the argument was the valid:-If 3 are II and U. are P then 3 are P.
10) Inconsistent use of terms. The predicate of the conclusion (i.e. 'prefer brunettes') is not to be found in either of the premises. Illicit process.
11) The logical form is valid:
All S are M. All M are P All S are P. Confusion is likely to arise as
to the meaning of the conclusion because of the term 'nothing but wisdom'.
It is an unclear term, so its truth/falsity would be most difficult
to establish. That 'the rich' have 'nothing but x' is what makes an
apparent contradiction in terms.
12) The terms in the conclusion are not the same as the terms in the
premises, therefore no logical inference is made. It appears to be and
inference, but it is not stated in a clearly unambiguous manner so that
the subject and predicate of premises and conclusion are sufficiently
equivalent in meaning. Shorn to its implied essentials the argument
might be presented as;-
'Priddy is the one who made the text The one who made the text is suspect
Therefore the text is suspect.'
However, the conclusion cannot alter the subject from that in the premises
without logical inconsistency. Illicit process.
13) Invalid conclusion. If p is included in u, then u is not necessarily included in p. The two classes may be co-extensive and thus be said
to include one another, but it is also possible that u includes more
than p.
14) Let 'those who disagree
with established authorities' = M
and 'those who are suffering from psychological complexes' = P
and 'those who think themselves capable of making up their own minds'=
S
then we have the logical form:- If all M are 3 and all M are P, the
all S are P.
The invalidity of this syllogism can be demonstrated by use of Venn's
diagrams as follows:- Here one can see that the conditions stated in
the premises are fulfilled in the diagram, but that the condition expressed
in the conclusion is not.
15) One can also see from the diagram that the conclusion 'some S are P' does follow with logical necessity from the premises. However, in both of the alternative conclusions stated in exercise 14) and 15) it should be noted that the subject has been altered from that of the premise... by the addition of the term 'think themselves'. Therefore there is illicit process in both cases, unless one can definitively also prove that those who think themselves capable of making up their own minds' also must always be the same as 'those who are capable of making up their own minds'.