(APPLIED IN SYLLOGISTIC LOGIC)
Inference, or reasoning logically,
is the deriving of one truth from others. This means that a 'new' proposition
(or statement) is accepted as true because the proposition is a valid
conclusion from propositions themselves accepted as true. 'Valid refers
to 'self-consistency' and is applied to the logical form of an
argument, not to its material contents. The distinction between
'form' and 'content' is essential to all logical reasoning, one which
will be made evident by examples in the following.
The principles of valid inference are fundamental and essential 'laws
of thought' or 'axioms' which underlie all valid reasoning. They are
not established by experience, being analytical statements and thus
being self-evident.
The three main principles
were formulated by Aristotle. A fourth principle given below, Leibnitz'
principle, is connected with experience and thus concerns material reasoning
rather than formal logic.
The Principle of Identity (A is A) stated briefly, means that the same term must always have the same meaning. The concept of Identity implies the concept of Diversity, because A is A is only significant because we refer to possible diversity.
The Principle of Contradiction
(A cannot both be B and not-B) means that of two contradictory assertions
about the same subject, both cannot be true - i.e. one must be false.
In other words, incompatible propositions cannot be true together.
This principle has previously been considered under the more accurate
or fitting title 'Principle of Non-Contradiction' . However, since the
other less explanatory usage is engrained, it is in this part of the
book named that accordingly. This principle is derived from that of
identity above.
Its application:-
(a) to the meaning of terms:- it secures the identical meaning of a
term by denying a term to be diverted to another meaning in the same
discourse.
b) to the mutual consistency of propositions: incompatible propositions
can not be true together.
The Principle of Excluded Middle (A either is, or is not, B)
denies that there can be any Intermediate alternative between truth
and falsity. Hence it refers to contradictories - and not contraries.
(Known traditionally as 'tertium non datur' or 'no third possibility
exists').
Its application:-
(a) to the meaning of a term:- any given meaning of a term either does,
or does not, belong to a given term in a given context.
(b) to the mutual consistency of propositions:- of relations between
classes and another limitation, namely that it only deals with relations
of identity and difference (or relations reducible to these) seems due
to the unnatural classification of propositions of the traditional doctrine.
In the first case the singular-termed proposition was forced to be considered
universal and, secondly, the only recognised relationship between terms
was the subject-attribute relation.
General Rules of
The Syllogism. (Relating to "structure")
I A syllogism must have three, and only three, terms
II A syllogism must have three, and only three, propositions (relating
to "quantity")
III The middle term must be distributed in at least one premise
IV No term may be distributed in the conclusion that is not distributed
in its premise (relating to "quality".
V At least one of the premises must be affirmative - (i.e. no conclusion
can follow from two negative premises)
VI A negative premise necessitates a negative conclusion, and a negative
conclusion must be preceded by a negative premise.
Corolloraries
VII Two particular premises give no valid conclusion
VIII A particular premise necessitates a particular conclusion
IX From a particular major and a negative minor nothing can be inferred.
The general rules of the syllogism are distinguished from the 'special
rules', which exist for each separate figure. The special rules depend
on the general rules, which in turn depend on the Laws or Principles
of Thought (i.e. Axioms of Reasoning). In the widest sense though, all
are interdependent.
A general description of
the requirement for a valid inference may be:-
A valid inference is the drawing of a conclusion that follows with
logical necessity from any two premises. (See also in the following
under 'valid conclusion' etc.)
(Note. The principles of logic are largely only illustrated here. For
an exhaustive statement of principles and derived logical rules, a fuller
study in logic should be sought.)
Strictly speaking, an inference cannot be invalid for it is then not
genuinely an inference. There occur apparently-valid inferences which,
on closer analysis, are seen not to follow with logical stringency from
the premises. These will be referred to hereafter as Invalid arguments
or invalid deductions. Deduction is the process of drawing a conclusion
from premises, whether by valid or invalid inference. A 'premise' is
always a categorical statement, but can be either particular or general.
It constitutes one of the grounds or reasons for the conclusion. At
least one premise in an argument will usually be general (called 'the
major premise') if the conclusion is to be valid in most types of argument.
'Logical necessity' means 'strict dependence upon clear and consistent
reasoning'. The description states a general rule of valid deduction,
which is specified by various sets of logical rules. Such rules are
developed with the stringency of mathematical reasoning. Different sets
of rules apply to different basic types of argument. In the following
the most common type of argument structure will mostly be considered,
those of 'class entailment', whereby the relations of inclusion and
exclusion between any two classes (of particulars) are examined systematically.
Deductive reasoning is of an overall hypothetical structure 'If a and b, then c'. The symbols 'a' and 'b' below stand for categorical statements.
Example of a 'class entailment'
argument (or 'traditional syllogism')
(a) If all humans are mortals (Major premise - general, categorical
statement)
(b) and if the Pope is human (Minor premise - particular categorical
statement)
(c) then the Pope is mortal. (Conclusion - particular categorical statement)
Here, an individual (the Pope) is included under the classes of humans
and mortals. The class 'humans' entails the class 'mortals' which in
turn entails all individuals, such as the Pope. The term 'entails' can
thus be interpreted as 'includes under' a class.
Ad 'logical form' and 'material content' of propositions;
Example:-
Suppose we 'abstract' the 'logical form' - from the 'material content':-Let
3 = logical subject of the conclusion, P = the logical predicate of
the conclusion and. M as the 'middle term' which is common to both premises.
We get:-
(a) If all M = P (Major premise) where El stands for the class 'all
humans'
(b) and S = M (Minor premise) and P for the class 'mortal'
(c) then S = P (Conclusion Valid) and S for the individual 'the Pope'.
This logical structure is known as a 'syllogism'. It is a valid structure
in this case, for it is logically necessary that, if the major and minor
premises are both true, the conclusion is also necessarily true. Whatever
definite classes or individuals are substituted for S, P and M, the
conclusion will always follow logically from the premises.
This is illustrated by Venn's diagram as follows:-
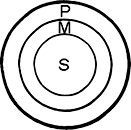 |
The class M is wholly included by the class P (P entails M). The individual S is wholly included by the class M (S is entailed by M). Therefore the individual S is wholly included by the class P also of necessity. (S is also entailed by P). Note that in the concrete example, M does not entail P, though P does entail M (i.e. there are other mortal beings than humans, such as animals). In other words M and P are not mutually entailed. M is thus represented within P. |
Consider the following argument:
(a) If all nuclear tests lead to radioactive pollution of the environment
(b) and some radioactive pollution of the environment leads to incurable
illnesses
(c) then some nuclear tests lead to incurable illnesses.
Abstracted we get:
| Where
M = 'lead to radioactive pollution of the environment' and S = 'nuclear tests' and P = 'lead to incurable illnesses', we get:- (a) If all S = M and (b) and some M = P (c) then some S = P |
With Venn's
diagrams we see either |
 |
or |  |
Since all S are included by M, but only some of M is included by P, it is possible for all of S to fall within M while falling outside P. Therefore the conclusion is not necessarily true as a result of the truth of the premises. This syllogistic structure is invalid, therefore. The truth of the conclusion cannot however be excluded, for some S might be included under P, but it is not logically entailed by P.
Consider also the example;
(a) If no bachelors are bigamists (True)
(b) and all men are bigamists (False)
(c) then no bachelors are men (False)
The structure of the above is:-
| Where
S = bachelors, M =bigamists and P = men, we get:- (a) If no S = M (b) and all P = M (c) then no S = P |
With Venn's
diagrams we see |
 |
but not |  |
because all P must be included under M. As the diagram on the left makes
clear, the logical structure is valid, the conclusion follows from the
premises with necessity even though the conclusion is false.
From this analysis we can
see to that if a logical structure that is valid has one true and
one false premise, the conclusion will sometimes be true, sometimes
be false. No logical necessity is involved here.
Even when both premises are false it is possible for a true conclusion
to be arrived at with a valid syllogism;-
(a) If no cats are mammals (False)
(b) & all mammals are dogs false)
(c) then no cats are dogs. (True and valid)
This means that one can sometimes arrive at a true statement on the
basis of false evidence, even by logical necessity. The premises in
any syllogism always have to be established independently by observation
(or by reasoning validly from true observation).
Another example of a valid syllogistic structure, this tine using the
(quantifier 'some' in one of the premises:-
(a) If no S = M
(b) and some P = U
(c) then some P = not-S To give a concrete example:- (a) If no gipsies
are blue-eyed
(b) and some travelling people are blue-eyed
(c) then some travelling people are not-gipsies.
Provided that it is true that there are no blue-eyed gipsies, and some
travelling people are blue-eyed, it must be true that some travelling
people are not gipsies. We cannot know from this however, whether the
conclusion is true or false until we know that both the premises are
true.
The foregoing gives a basis for defining the distinction between validity
and truth. A valid conclusion is one the correctness of which follows
with logical necessity from other statements. (i.e. a logical conclusion
from premises, or a valid analytic statement).
A true statement is a synthetic statement which is verifiable by observation. Similarly, an invalid conclusion's incorrectness follows with logical necessity from some other statements.(i.e.- from premises or definitions. An invalid analytic statement would thus be an invalid conclusion from a definition or a rule of language usage).
False statements are synthetic
statements which are falsifiable by observation (such as untruths,
lies or erroneous statements of fact). Further, there are unverifiable
statements, being those which cannot be tested by some form of observation,
even though they are synthetic and thus can be either true or false.
Other types of logical
argumentation
The proceeding gives a general outline of various central concepts and
methods in that area of logic known as syllogistic logic, which is logic
in its traditional meaning, being largely identical with Aristotle's
logic logic (developed into so-called 'traditional logic'). An equally
fundamental area of logic is usually known as 'prepositional logic'
or 'prepositional calculus'. This represents a special formal language
in which propositions are expressed so as to exhibit their logical form
- as distinct from their logical content - in a yet more abbreviated
manner than here employed. The purpose of prepositional logic is to
provide clear standards of meaning and validity of inference according
to which sentences (with content) can be translated into formal propositions
(with form only) for evaluation as to their truth value. For example,
the conjunctive terms 'and', 'or', 'not', 'if and 'then' are formalised,
which is to say that their use is fixed by logical convention for the
purposes of overview of their logical meaning when they occur in complex
series of reasoning. Part of prepositional logic is made up of what
Aristotle analysed as hypothetical, disjunctive and alternative arguments.
At a more general level of logical theory, quantification theory arises.
This theory forms a general basis for both prepositional and syllogistic
logic. It widens the scope of syllogistic logic by allowing the analysis
of arguments with class quantifiers other than the three basic quantifiers
permissible in syllogistic logic (i.e. All, none and Some)
At a yet more general or embracing level are the logical theories of
identity and quantity.
EXERCISES (VALID INFERENCE)
1) What can be validly deduced from the following two premises, if anything?
(a) If every U.S. President was a male
(b) and a movie actor was U.S. President
(c) then…
Explain why you consider your conclusion valid or invalid.
2) If indiscriminate spending is a proof of ignorance of what money
and goods really represent and if Christmas shopping frequently is indiscriminate
spending, then... what can validly be deduced from this, if anything?
Give reasons for your conclusion's validity or invalidity.
3) Analyse the following syllogistic structure by the aid of Venn's
diagrams and answer whether a valid conclusion can be obtained from
it and whether you consider the syllogism logically valid;-
All S are M
and Some M are P
then Some S are P.
SOLUTIONS TO EXERCISES IN
VALID INFERENCE
1) One can validly conclude that 'a movie actor was a male''
- which also happens to be true. The reverse is true but invalid (i.e.
that 'a male was a movie actor'). The validity of this syllogism can
be demonstrated by abstracting the logical form of the argument and
showing the necessary relationship between the individuals and classes
involved as follows:-
The logical form of the argument is the syllogism:-
| If all M was S and P was M then P was S (but not S was P) |
this is satisfied by the diagram:- |  |
2) The argument is:- If Christmas shopping frequently is indiscriminate spending and indiscriminate spending is a proof of ignorance of what money and goods really represent then Christmas shopping frequently is proof of ignorance of what money and goods really represent The logical form is valid as follows:-
| If S is M and M is P then S is P |
this is satisfied by the diagram:- |  |
If S is M
and M is P
then S is P this is satisfied by the diagram:- If the premises are true,
then the truth of the conclusion follows with necessity. However one
interprets the first premise, it seems likely to be true, the only problem
possibly being the word 'frequently'. Whether the second premise is
true will depend upon how it is interpreted, and it is open to a variety
of interpretations. Therefore the truth of the conclusion must remain
in doubt, despite its logical validity.
3) The logical form is invalid. This can be demonstrated by showing
that some of the class of M can contain two distinct and separate sub-classes
S and P as follows:-
 |
 |
Both the above diagrams show how S and P can exclude each other, while
the following shows how it is possible but not necessary for
'some S to be P'.
 |